R: Bioestatística I
Fazer uma análise estatística completa usando RStudio pode ser um processo complexo e abrangente. A análise estatística é um campo vasto, com muitas técnicas e métodos diferentes disponíveis.
A escolha das técnicas corretas dependerá do seu conjunto de dados, das perguntas de pesquisa e dos objetivos da análise. Consultar a documentação dos pacotes e recursos adicionais de estatística pode ser útil para aprofundar-se em análises mais avançadas. Na parte I, focaremos na estatística descritiva dos dados.
Importando dados
Para este estudo, utilizaremos os conjuntos de dados mtcars e meusdados que será criado utilizando números e letras aleatórios
data(mtcars) #Dados do próprio R
str(mtcars) #Resumo dos dados
#Criando um conjunto de dados próprio
set.seed(150) #Utilizando esta função, podemos preservar sempre os mesmos valores aleatórios
meusdados <- data.frame(aleatorio = sample(150), norm = rnorm(150, mean=10, sd=3))
locais <- rep(letters[1:5], each = 30) #Criando um objeto com diferentes locais
#letters pode ser utilizado para produzir letras do alfabeto
locais <- sample(locais, 150)#Criando uma ordem aleatória para o objeto local
meusdados$locais <- locais #Atribuindo nosso objeto a uma variável no nosso dataframe meus dados
Medidas de Tendência Central
As medidas de tendência central ou posição são ferramentas que resumem um conjunto de dados observados em um único valor representativo da variável em análise. Geralmente, uma das seguintes medidas de tendência central é usada: média, mediana ou moda.
Media aritmética
A média aritmética simples é a medida mais comum de tendência central para resumir conjuntos de dados, calculada como a soma das observações dividida pelo número delas.
mean(meusdados$aleatorio) #Utilizando a função mean para calcular a média aritmética
mean(mtcars$mpg) #Utilizando um conjunto de dados do R
mean(c(1,4,2,6)) #Utilizando apenas números definidos
Podemos explorar as estatísticas descritivas básicas com a função apply ou tapply:
apply(X = mtcars[ ,2:4], MARGIN = 2, FUN = mean) #O argumento margin na função apply em R especifica a direção ao longo da qual você deseja aplicar uma função a uma matriz ou array. Você pode definir margin como 1 para aplicar a função ao longo das linhas, como 2 para aplicá-la ao longo das colunas, ou c(1, 2) para aplicá-la a todas as combinações possíveis de linhas e colunas. Se a matriz tiver nomes de dimensões (EX: nome para a variável como cyl), você pode usar esses nomes no argumento margin para selecionar dimensões específicas para a aplicação da função. Em resumo, margin controla a direção em que a função é aplicada a dados multidimensionais. No argumento X, quando seleciono apenas [,2:4], é especificado que só preciso da média destas colunas(2 a 40.
#Veja mais em ?apply
apply(mtcars[ ,c("cyl", "disp", "hp")], 2, mean) #Outra maneira de especificar as colunas
tapply(meusdados$norm, meusdados$locais, mean) #Utilizando a função tapply para verificar a média em relação aos locais
Mediana
A mediana é o valor central de um conjunto de dados ordenados. Quando há um número ímpar de observações, a mediana é a observação central; com um número par, é a média das duas observações centrais.
median(meusdados$aleatorio)
Podemos explorar as estatísticas descritivas básicas com a função apply ou tapply:
apply(X = mtcars[ ,2:4], MARGIN = 2, FUN = median)
apply(mtcars[ ,c("cyl", "disp", "hp")], 2, median)
tapply(meusdados$norm, meusdados$locais, median)
Interpretações da média e mediana
Quando a média é significativamente diferente da mediana, isso geralmente indica que a distribuição dos dados está inclinada ou assimétrica. Aqui estão algumas interpretações comuns:
Média maior do que a mediana: Isso sugere que a distribuição dos dados é assimétrica positiva (à direita). Isso significa que existem valores extremamente altos que estão puxando a média para cima, enquanto a mediana permanece mais próxima dos valores centrais. Exemplos disso podem ser encontrados em distribuições de renda, onde algumas pessoas têm rendas muito altas, distorcendo a média.
Média menor do que a mediana: Nesse caso, a distribuição dos dados é assimétrica negativa (à esquerda). Valores extremamente baixos puxam a média para baixo, enquanto a mediana permanece mais próxima dos valores centrais. Um exemplo pode ser uma classe de estudantes, onde a maioria das notas é alta, mas alguns alunos obtiveram pontuações muito baixas.
A mediana é menos sensível a valores extremos porque não leva em consideração o valor exato desses extremos, apenas sua posição no conjunto ordenado de dados. Em contraste, a média considera todos os valores, o que a torna mais sensível a valores extremos.
Quanto à média truncada, o uso do argumento trim na função mean permite calcular a média excluindo uma porcentagem especificada dos valores extremos, ajudando a reduzir o impacto desses valores na média. Isso pode ser útil quando você deseja obter uma medida mais robusta da tendência central, especialmente em dados com valores atípicos ou extremos.
apply(mtcars[ ,c("cyl", "disp", "hp")], 2, mean) #Média
apply(mtcars[ ,c("cyl", "disp", "hp")], 2, median) #Mediana
apply(mtcars[ ,c("cyl", "disp", "hp")], 2,trim= 0.1, mean) #Com essa alteração no parâmetro trim, é possível verificar que os valores da média tiveram uma aproximação da mediana na maioria das variáveis, possívelmente pela remoção de alguns outliers.
O trim retira do cálculo da média os valores extremos com o corte definido pelo fator estipulado a partir das observações extremas. Nesse caso, retiramos 10% dos maiores valores e 10% dos menores. Como a média é muito sensível a valores extremos, se houver algum valor muito grande ou pequeno em relação ao resto, a média truncada seria bem diferente da média com todos os dados.
Quantis
Os quantis são uma maneira útil de entender como os valores estão distribuídos em um conjunto de dados. Eles dividem os dados em quatro partes iguais depois de serem ordenados. O primeiro quartil (Q1) marca o limite entre os 25% menores valores e os 75% maiores valores. O segundo quartil (Q2) é a mediana, que separa os dados em duas partes iguais, com 50% abaixo e 50% acima. O terceiro quartil (Q3) é o limite entre os 75% menores valores e os 25% maiores valores.
Ao usar a função summary em um vetor de dados numéricos, você obtém uma visão rápida desses valores, incluindo o mínimo, o primeiro quartil, a mediana (segundo quartil), o terceiro quartil e o máximo. Isso é útil para entender a distribuição dos dados, identificar possíveis valores atípicos e verificar a simetria da distribuição.
Se os quartis estiverem igualmente espaçados, isso sugere uma distribuição simétrica. Se, por outro lado, os quartis estiverem deslocados em relação à mediana, isso pode indicar uma distribuição assimétrica. Essas informações ajudam os analistas de dados a ter uma compreensão mais completa da natureza dos dados com os quais estão trabalhando.
quantile(meusdados$aleatorio)
summary(meusdados$aleatorio)
quantile(meusdados$aleatorio, probs = seq(from = 0, to = 1, by = 0.1))#O argumento probs da função quantile permite retornar o valor de qualquer quantil, vamos separar os dados em 10 quantis, com 10% dos dados em cada quantil.
Moda
A moda de um conjunto de valores é o valor que ocorre com mais frequência. Se dois valores têm a mesma frequência máxima, o conjunto é chamado de bimodal. Se mais de dois valores têm a mesma frequência máxima, o conjunto é multimodal. Quando nenhum valor se repete, o conjunto não tem moda (é amodal). É possível calcular a moda, mesmo para variáveis qualitativas.
tab = table(mtcars$cyl)
moda = names(tab)[tab == max(tab)]#O valor 8 é o que mais aparece
print(moda)
Máximo e mínimo
Máximo maior valor observado no conjunto de dados e mínimo é o menor valor.
max(meusdados$aleatorio) #Máximo para a variável aleatorio
(tapply(meusdados$aleatorio, meusdados$locais, max)) #Máximo para cada local
min(meusdados$aleatorio) #Mínimo para a variável aleatorio
(tapply(meusdados$aleatorio, meusdados$locais, min)) #Mínimo para cada local
Máximo maior valor observado no conjunto de dados e mínimo é o menor valor.
Medidas de dispersão
As medidas de dispersão são usadas para avaliar o quanto os dados estão espalhados ou afastados em relação ao valor médio (ou medida de tendência central). Elas fornecem informações importantes sobre a variabilidade ou a dispersão dos dados em um conjunto. Algumas das medidas de dispersão mais comuns incluem:
Amplitude
A diferença entre o maior e o menor valor em um conjunto de dados. É uma medida simples de dispersão, mas pode ser sensível a valores extremos.
amplitude_aleatorio = max(meusdados$aleatorio) - min(meusdados$aleatorio)
amplitude_norm <- diff(range(meusdados$norm)) #Outra maneira de fazer usando a função range
# Resultados
amplitude_aleatorio
amplitude_norm
Variância
Uma medida que avalia o quão distantes os valores individuais estão da média. Ela leva em consideração todos os valores no conjunto e é mais robusta contra valores extremos.
var_aleatorio <- var(meusdados$aleatorio)
var_norm <- var(meusdados$norm)
#Por tratamentos
variancias = tapply(meusdados$aleatorio, meusdados$locais, var)
# Resultados
var_aleatorio
var_norm
variancias
Desvio Padrão
A raiz quadrada da variância. Ele também fornece uma medida da dispersão dos dados, mas está na mesma unidade de medida dos dados originais, tornando-o mais interpretável. É uma medida descritiva geralmente usada com a média.
sd_aleatorio <- sd(meusdados$aleatorio)
sd_norm <- sd(meusdados$norm)
# Resultados
sd_aleatorio
sd_norm
Intervalo Interquartil (IQR)
A diferença entre o terceiro quartil (Q3) e o primeiro quartil (Q1) de um conjunto de dados ordenados. O IQR é útil para avaliar a dispersão dos valores centrais e é menos afetado por valores extremos. É uma medida descritiva geralmente usada com a mediana.
iqr_aleatorio <- IQR(meusdados$aleatorio)
iqr_norm <- IQR(meusdados$norm)
# Resultados
iqr_aleatorio
iqr_norm
Coeficiente de Variação (CV)
Uma medida relativa de dispersão que expressa a variabilidade como uma porcentagem da média. É útil para comparar a dispersão em conjuntos de dados com diferentes escalas.
cv_aleatorio <- sd(meusdados$aleatorio) / mean(meusdados$aleatorio) * 100
cv_norm <- sd(meusdados$norm) / mean(meusdados$norm) * 100
# Resultados
cv_aleatorio
cv_norm
Essas medidas de dispersão ajudam os analistas de dados a entender a variabilidade intrínseca nos dados, identificar valores atípicos e avaliar a consistência ou a dispersão dos dados em relação à média.
Quarteto de Anscombe
Este conjunto de dados é composto de 4 pares de variáveis, nomeadas x1 a x4 (variáveis independentes ou preditoras) e y1 a y4 (variáveis dependentes ou resposta). Abaixo, esses dados serão explorados e o output demonstrado. Atente-se as interpretações que podem ser feitas a partir dos resultados de cada análise:
data("anscombe")
names(anscombe) #Visualizando os nomes das variáveis
str(anscombe) #Visualizando um resumo
'data.frame': 11 obs. of 8 variables:
$ x1: num 10 8 13 9 11 14 6 4 12 7 ...
$ x2: num 10 8 13 9 11 14 6 4 12 7 ...
$ x3: num 10 8 13 9 11 14 6 4 12 7 ...
$ x4: num 8 8 8 8 8 8 8 19 8 8 ...
$ y1: num 8.04 6.95 7.58 8.81 8.33 ...
$ y2: num 9.14 8.14 8.74 8.77 9.26 8.1 6.13 3.1 9.13 7.26 ...
$ y3: num 7.46 6.77 12.74 7.11 7.81 ...
$ y4: num 6.58 5.76 7.71 8.84 8.47 7.04 5.25 12.5 5.56 7.91 ...
Comparando as médias das variáveis do objeto anscombe:
apply(anscombe[1:4], MARGIN = 2, FUN = mean)
apply(anscombe[5:8], 2, mean)
x1 x2 x3 x4
9 9 9 9
y1 y2 y3 y4
7.500909 7.500909 7.500000 7.500909
Agora, observando as variâncias:
apply(anscombe[1:4], 2, var)
apply(anscombe[5:8], 2, var)
x1 x2 x3 x4
11 11 11 11
y1 y2 y3 y4
4.127269 4.127629 4.122620 4.123249
A questão central para este conjunto de dados é determinar se existe uma relação entre cada variável x e y. Essa relação pode ser avaliada usando o coeficiente de correlação de Pearson, que varia de zero (indicando nenhuma correlação) a um (indicando uma correlação perfeita, seja positiva ou negativa).
cor(anscombe$x1, anscombe$y1)
[1] 0.8164205
O código acima pode ser aplicado através da função with que facilita a digitação das variáveis:
with(anscombe, cor(x1, y1))
with(anscombe, cor(x2, y2))
with(anscombe, cor(x3, y3))
with(anscombe, cor(x4, y4))
[1] 0.8164205
[1] 0.8162365
[1] 0.8162867
[1] 0.8165214
Outra maneira de avaliar a relação é com os coeficientes da reta de um modelo linear entre as duas variáveis. Essa relação é obtida pela função coef aplicada ao um objeto de modelo linear. Vamos avaliar esse coeficientes para os quatro conjuntos de variáveis:
(coef1 <- coef(lm(y1 ~ x1, data = anscombe)))
(coef2 <- coef(lm(y2 ~ x2, data = anscombe)))
(coef3 <- coef(lm(y3 ~ x3, data = anscombe)))
(coef4 <- coef(lm(y4 ~ x4, data = anscombe)))
(Intercept) x1
3.0000909 0.5000909
(Intercept) x2
3.000909 0.500000
(Intercept) x3
3.0024545 0.4997273
(Intercept) x4
3.0017273 0.4999091
Todos os coeficientes estão muito próximos a 3.00 e 0.50. Vamos criar os gráficos de dispersão entre as variáveis x e y para os quatro casos e vamos incluir a relação linear para cada par com a função abline. Nossa única inclusão no plot foram os argumentos xlim e ylim para que todos os gráficos tenham as mesmas escalas nos eixos:
par(mfrow = c(2, 2)) # 4 graficos em uma janela
plot(y1 ~ x1, data = anscombe,
xlim = range(anscombe[,1:4]), ylim = range(anscombe[,5:8]))
abline(coef1)
plot(y2 ~ x2, data = anscombe,
xlim = range(anscombe[,1:4]), ylim = range(anscombe[,5:8]))
abline(coef2)
plot(y3 ~ x3, data = anscombe,
xlim = range(anscombe[,1:4]), ylim = range(anscombe[,5:8]))
abline(coef3)
plot(y4 ~ x4, data = anscombe,
xlim = range(anscombe[,1:4]), ylim = range(anscombe[,5:8]))
abline(coef4)
par(mfrow=c(1,1))
#O uso de xlim e ylim com um determinado range é uma estratégia usada para controlar a escala dos gráficos gerados. No contexto do código fornecido, o objetivo é garantir que todos os gráficos de dispersão tenham os mesmos limites nos eixos x e y. Isso é importante porque o conjunto de dados anscombe contém quatro pares de conjuntos de dados (x, y) que podem ter diferentes faixas de valores.
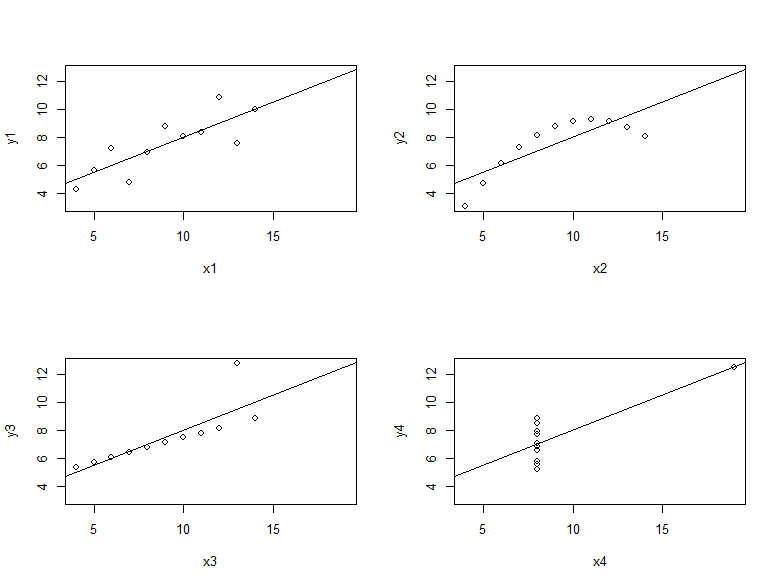
Este conjunto de dados foi criado por Frank Anscombe, um estatístico renomado, com o propósito de destacar a importância da análise visual de dados, conforme pode ser visto aqui. Durante nossa análise exploratória não gráfica, notamos que as médias, desvios-padrão, correlações e coeficientes de regressão são praticamente idênticos para os quatro conjuntos de dados, sugerindo que eles são semelhantes em termos estatísticos. No entanto, é notável como eles diferem substancialmente em termos visuais e de interpretação:
- O primeiro conjunto de dados parece seguir as suposições dos modelos lineares, mostrando uma relação linear entre as variáveis.
- O segundo conjunto de dados exibe uma clara relação não linear entre as variáveis.
- O terceiro conjunto de dados possui um valor atípico influente que afeta a inclinação da relação e introduz uma heterogeneidade na variância.
- O quarto conjunto de dados também possui um ponto atípico de alta alavancagem que é crítico para a relação entre as variáveis; caso seja removido da amostra, as variáveis y4 em função de x4 não apresentarão mais nenhuma relação aparente.
Essas observações enfatizam a importância de não depender apenas de estatísticas resumidas e ressaltam como a análise visual pode revelar informações cruciais sobre os dados.
Acesse a sessão gráficos neste site e aprenda como explorar visualmente seus dados!
Exercícios
A- Utilizando os dados mtcars calcule a média e a mediana das seguintes variáveis: “mpg” “cyl” “disp” “hp” “drat”.
B- Descubra a moda da variável “qsec” e “vs” em mtcars.
C- Calcule a amplitude da variável “carb” em mtcars.
d- Descubra a correlação e represente graficamente considerando 8 variáveis de mtcars (semelhante ao que foi demonstrado com Anscombe).


