R: Bioestatística II
Fazer uma análise estatística completa usando RStudio pode ser um processo complexo e abrangente. A análise estatística é um campo vasto, com muitas técnicas e métodos diferentes disponíveis.
A escolha das técnicas corretas dependerá do seu conjunto de dados, das perguntas de pesquisa e dos objetivos da análise. Consultar a documentação dos pacotes e recursos adicionais de estatística pode ser útil para aprofundar-se em análises mais avançadas. Na parte II, observaremos alguns testes estatísticos.
Importando dados
Para este estudo, utilizaremos os conjuntos de dados mtcars, meusdados que será criado utilizando números e letras aleatórios, butterfat e ToothGrowth, conforme indicado abaixo.
data(mtcars) #Dados do próprio R
str(mtcars) #Resumo dos dados
#Criando um conjunto de dados próprio
set.seed(150) #Utilizando esta função, podemos preservar sempre os mesmos valores aleatórios
meusdados <- data.frame(aleatorio = sample(150), norm = rnorm(150, mean=10, sd=3))
locais <- rep(letters[1:5], each = 30) #Criando um objeto com diferentes locais
#letters pode ser utilizado para produzir letras do alfabeto
locais <- sample(locais, 150)#Criando uma ordem aleatória para o objeto local
meusdados$locais <- locais #Atribuindo nosso objeto a uma variável no nosso dataframe df
table(meusdados$locais) #Visualizando com a função table
summary(meusdados)
if(!require(faraway)) install.packages("faraway")
library(faraway)
data(butterfat)
str(butterfat)
data("ToothGrowth")
ToothGrowth$supp <- factor(ToothGrowth$supp)
ToothGrowth$dose <- factor(ToothGrowth$dose)
str(ToothGrowth)
a b c d e
30 30 30 30 30
aleatorio norm locais
Min. : 1.00 Min. : 2.697 Length:150
1st Qu.: 38.25 1st Qu.: 7.813 Class :character
Median : 75.50 Median :10.194 Mode :character
Mean : 75.50 Mean : 9.987
3rd Qu.:112.75 3rd Qu.:12.096
Max. :150.00 Max. :17.238
'data.frame': 100 obs. of 3 variables:
$ Butterfat: num 3.74 4.01 3.77 3.78 4.1 4.06 4.27 3.94 4.11 4.25 ...
$ Breed : Factor w/ 5 levels "Ayrshire","Canadian",..: 1 1 1 1 1 1 1 1 1 1 ...
$ Age : Factor w/ 2 levels "2year","Mature": 2 1 2 1 2 1 2 1 2 1 ...
'data.frame': 60 obs. of 3 variables:
$ len : num 4.2 11.5 7.3 5.8 6.4 10 11.2 11.2 5.2 7 ...
$ supp: Factor w/ 2 levels "OJ","VC": 2 2 2 2 2 2 2 2 2 2 ...
$ dose: Factor w/ 3 levels "0.5","1","2": 1 1 1 1 1 1 1 1 1 1 ...
Testes pré-requisitos
Avaliar a normalidade e a homogeneidade dos dados é fundamental antes de realizar análises estatísticas, pois esses critérios influenciam diretamente na validade e interpretação dos resultados estatísticos. Abaixo, observe como realizar estes testes no R.
Normalidade – Shapiro-Wilk
O teste de Shapiro-Wilk, realizado com a função shapiro.test() no R, é usado para verificar se uma variável segue uma distribuição normal (gaussiana). Isso é importante pois a normalidade é um pre-requisito de certos testes estatístico. como a análise de variância (ANOVA) ou o teste t.
A interpretação do resultado do teste de Shapiro-Wilk envolve a análise do valor-p. Aqui está como interpretar o teste de Shapiro-Wilk:
Hipótese Nula (H0): A hipótese nula afirma que os dados seguem uma distribuição normal.
Hipótese Alternativa (H1): A hipótese alternativa sugere que os dados não seguem uma distribuição normal.
A interpretação do resultado baseia-se no valor-p associado ao teste:
Se o valor-p for maior que o nível de significância (geralmente definido em 0,05 ou 0,01), você não rejeita a hipótese nula (H0). Se o valor-p for menor que o nível de significância escolhido, você rejeita a hipótese nula (H0).Ou seja nos testes de normalidade, consideramos que os dados seguem distribuição normal quando p é maior que 0.05.
shapiro.test(meusdados$norm)# p = 0.614, Normal
Shapiro-Wilk normality test
data: meusdados$norm
W = 0.99244, p-value = 0.614
Em resumo, o teste de Shapiro-Wilk é usado para verificar a normalidade dos dados. Se o valor-p for baixo, você pode concluir que os dados não são normalmente distribuídos, o que pode afetar a escolha do método estatístico apropriado para a análise. Se o valor-p for alto, você pode continuar com a suposição de que os dados são aproximadamente normais para fins de análise paramétrica.
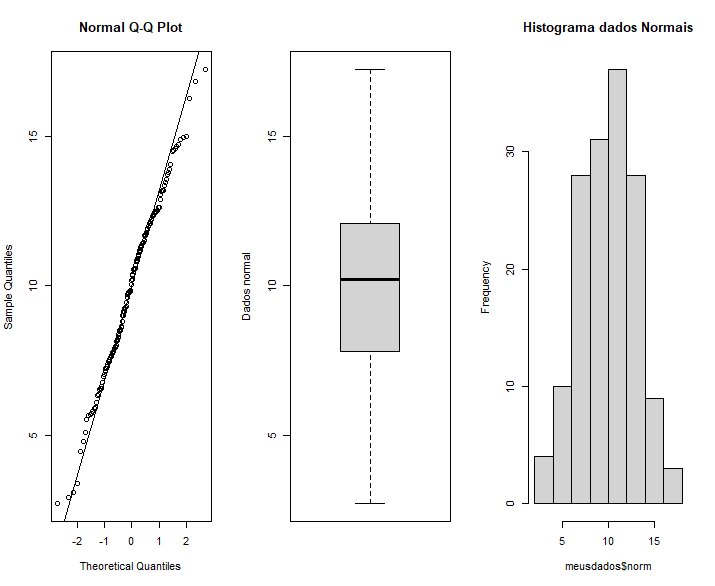
Visualização:
par(mfrow=c(1,3))
qqnorm(meusdados$norm)
qqline(meusdados$norm)
boxplot(meusdados$norm, ylab = "Dados normal")
hist(meusdados$norm, main = "Histograma dados Normais")
par(mfrow=c(1,1))
Homogeneidade de variâncias – Levene (pacote car)
Pacote:
if(!require(car)) install.packages("car")
library(car)
O teste de Levene é uma técnica estatística usada para verificar a homogeneidade das variâncias entre grupos em uma análise de variância (ANOVA) ou em outras análises estatísticas. Ele é utilizado para avaliar se as variâncias das diferentes amostras ou grupos são estatisticamente iguais ou diferentes. A hipótese nula (H0) do teste de Levene afirma que todas as amostras têm variâncias iguais, enquanto a hipótese alternativa (H1) sugere que pelo menos uma amostra tem uma variância diferente das outras.
Aqui está como interpretar o resultado do teste de Levene:
Hipótese Nula (H0): A hipótese nula assume que todas as amostras têm variâncias iguais.
Hipótese Alternativa (H1): A hipótese alternativa sugere que pelo menos uma amostra tem uma variância diferente das outras.
A interpretação do resultado do teste de Levene envolve a análise do valor-p:
Valor-p (p-value): O valor-p é a probabilidade de obter uma estatística de teste F tão extrema quanto a observada, sob a suposição de que todas as amostras têm a mesma variância (hipótese nula). Quanto menor o valor-p, mais forte é a evidência contra a hipótese nula.
Se o valor-p for maior que o nível de significância escolhido (geralmente definido em 0,05 ou 0,01), você não rejeita a hipótese nula (H0). Isso sugere que não há evidências estatisticamente significativas para concluir que as variâncias são diferentes entre as amostras. Você pode assumir que a homogeneidade de variâncias é atendida.
Se o valor-p for menor que o nível de significância, você rejeita a hipótese nula e conclui que há evidências estatisticamente significativas de que pelo menos uma amostra tem uma variância diferente das outras. Nesse caso, você deve considerar métodos estatísticos alternativos que levem em conta essa falta de homogeneidade de variância.
Em resumo, o teste de Levene é usado para verificar a homogeneidade de variâncias entre grupos. A interpretação do valor-p ajuda a determinar se essa suposição foi atendida ou não, o que é importante em análises estatísticas, para garantir que os resultados sejam confiáveis.
leveneTest(Butterfat ~ Age, data = butterfat, center=mean) #p > 0,05 Isso significa que a suposição de homogeneidade de variância foi atendida
Levene's Test for Homogeneity of Variance (center = mean)
Df F value Pr(>F)
group 1 0.041 0.8401
98
A seguir, vamos discutir alguns testes estatísticos que necessitam que os dados (ou resíduos) sigam uma distribuição normal e/ou homogeneidade das variâncias como um pré-requisito.
Modelo teste t para uma amostra
O teste t para uma amostra é uma análise estatística usada para determinar se a média de uma única amostra é estatisticamente diferente de um valor de referência conhecido ou hipotético. Ele avalia se existe evidência estatística para afirmar que a média da amostra é significativamente diferente do valor esperado. Isso é feito comparando a média da amostra com um valor de referência e levando em consideração o tamanho da amostra e o desvio padrão da população.
t.test(meusdados$norm, mu = 10) # Comparando através do teste T se a média é igual a 10 em termos estatísticos. Neste caso as médias são iguais, pois p valor é > 0,05.
One Sample t-test
data: meusdados$norm
t = -0.0564, df = 149, p-value = 0.9551
alternative hypothesis: true mean is not equal to 10
95 percent confidence interval:
9.51422 10.45882
sample estimates:
mean of x
9.986519
t – Estatística t (t-statistic):(t = -0.0564) A estatística t é calculada dividindo a diferença média (mean of the differences) pela estimativa do erro padrão das diferenças. Ela quantifica a magnitude da diferença entre as duas amostras em termos de desvios padrão. Quanto maior for a estatística t, maior será a diferença relativa entre as amostras.
df – Graus de Liberdade (degrees of freedom): (df = 149) Os graus de liberdade são usados para calcular o valor-p e indicam quantos graus de liberdade estão disponíveis para o teste estatístico. No caso de um teste t pareado, os graus de liberdade são determinados pelo número de pares de observações menos 1.
p-value – Valor-p: (p-valor = 0.9551)O valor-p é a probabilidade de obter um resultado tão extremo ou mais extremo do que o observado, sob a hipótese nula de que não há diferença real entre as duas amostras. É uma medida que nos ajuda a determinar a significância estatística do resultado.
Se o valor-p for menor que o nível de significância pré-definido (geralmente 0,05 ou 0,01), rejeitamos a hipótese nula (H0) e concluímos que existe uma diferença estatisticamente significativa entre as amostras. Em outras palavras, há evidências de que a mudança observada é estatisticamente significativa.
Se o valor-p for maior que o nível de significância, não temos evidências estatísticas para rejeitar a hipótese nula, o que sugere que não há diferença estatisticamente significativa entre as amostras.
conf.int – é o intervalo de confiança da média a 95% (conf.int = [9.51422, 10.45882]),
sample estimates é o valor médio da amostra (média = 9.986519).
Teste-t independente
O teste t independente, também conhecido como teste t de Student para amostras independentes, é uma técnica estatística usada para comparar as médias de duas amostras independentes e determinar se existe uma diferença estatisticamente significativa entre elas. Esse teste é apropriado quando você deseja comparar duas amostras diferentes, como dois grupos de pessoas, dois grupos de produtos ou duas populações independentes, e verificar se a diferença nas médias é devida ao acaso ou se é estatisticamente significativa.
Uma variável dependente (resposta) continua e uma variável independente (explanatória) categórica com dois grupos/níveis com unidades amostrais independentes (indivíduos diferentes em cada grupo/nível).
Normalidade por grupo
shapiro.test(butterfat$Butterfat[butterfat$Age=="2year"]) #Não normal, pois p <0,05. Continuaremos com as análises para fins didáticos. Consulte o conteúdo extra Normalização Box-Cox para mais.
shapiro.test(butterfat$Butterfat[butterfat$Age=="Mature"]) #Normal
Shapiro-Wilk normality test
data: butterfat$Butterfat[butterfat$Age == "2year"]
W = 0.95067, p-value = 0.03634
Shapiro-Wilk normality test
data: butterfat$Butterfat[butterfat$Age == "Mature"]
W = 0.9712, p-value = 0.2589
Visualização normalidade:
par(mfrow=c(1,3))
qqnorm(butterfat$Butterfat[butterfat$Age=="2year"], main="2year")
qqline(butterfat$Butterfat[butterfat$Age=="2year"])
qqnorm(butterfat$Butterfat[butterfat$Age=="Mature"], main="Mature")
qqline(butterfat$Butterfat[butterfat$Age=="Mature"])
boxplot(Butterfat ~ Age, data = butterfat)
par(mfrow=c(1,1))
#Para visualizar o quanto os dados se aproximam da normalidade.
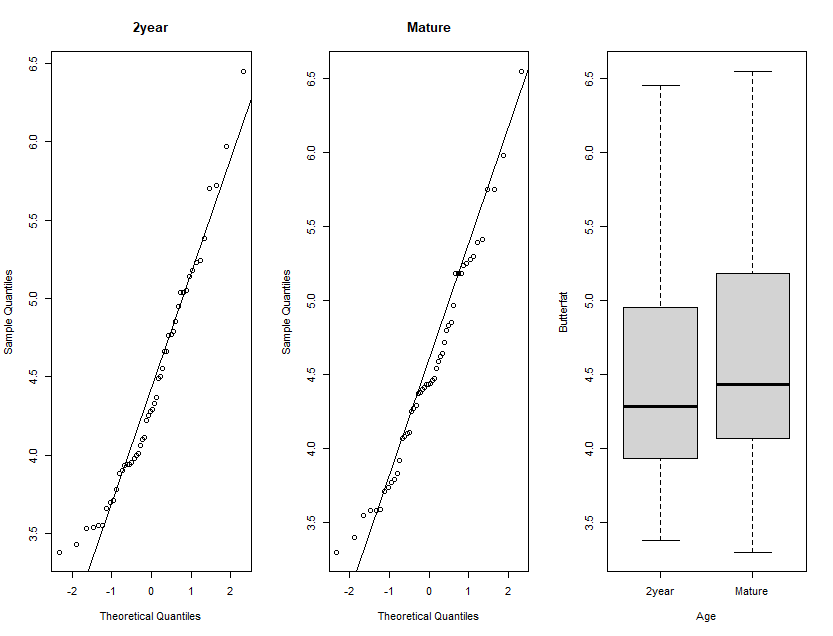
Teste:
t.test(Butterfat ~ Age, data = butterfat, var.equal=TRUE)
#Neste caso, não há diferenças entre os grupos analisados.
Two Sample t-test
data: Butterfat by Age
t = -0.72918, df = 98, p-value = 0.4676
alternative hypothesis: true difference in means between group 2year and group Mature is not equal to 0
95 percent confidence interval:
-0.3892704 0.1800704
sample estimates:
mean in group 2year mean in group Mature
4.4298 4.5344
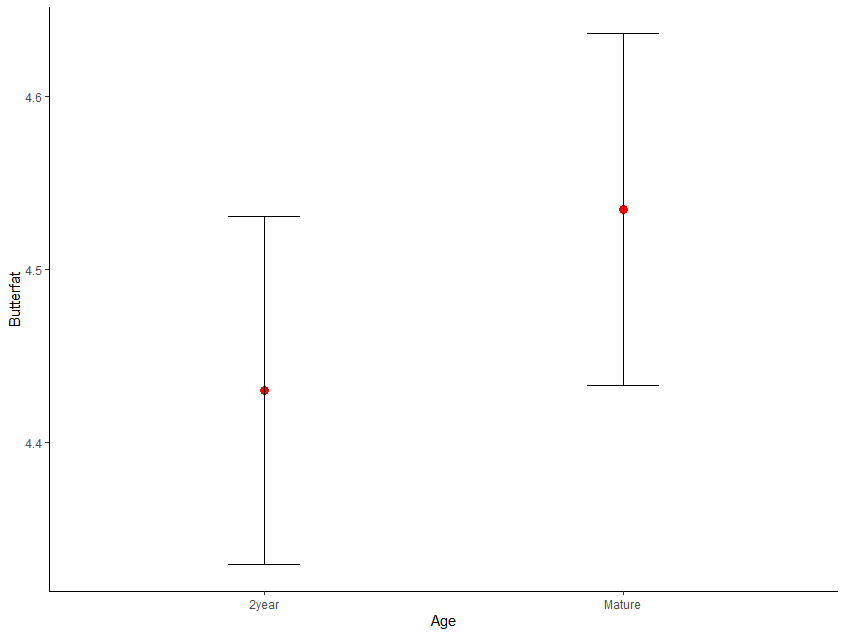
Visualização:
if(!require(ggplot2)) install.packages("ggplot2") #Para instalar caso ainda não tenha utilizado anteriormente
library(ggplot2)
ggplot(butterfat, aes(x = Age, y = Butterfat)) + #(dados, aes(x= dados para o eixo x, y= dados para o eixo Y))
stat_summary(fun = "mean", geom = "point", size = 3, color = "red") + # Ponto que representa a média, a função stat_summary realiza a computação da média dos dados, geom define qual é o símboo utilizado, size e color são para personalização do mesmo.
stat_summary(fun.data = "mean_se", geom = "errorbar", width = 0.2) + # Barras de erro com base no erro padrão, mean_se é o argumento utilizado para isto
labs(x = "Age", y = "Butterfat") + theme_classic() # Labs adiciona os rótulos aos eixos e Theme_classic() Adiciona um tema clássico ao gráfico
Teste-t pareado
Aqui estão os principais conceitos e etapas envolvidos na realização e interpretação de um teste t pareado:
Hipótese Nula (H0): A hipótese nula assume que não há diferença significativa entre as médias das duas amostras relacionadas. Em outras palavras, as médias são iguais.
Hipótese Alternativa (H1): A hipótese alternativa sugere que há uma diferença significativa entre as médias das duas amostras relacionadas. Em outras palavras, as médias são diferentes.
Diferenças (differences): No teste t pareado, você calcula as diferenças entre as observações emparelhadas (por exemplo, as diferenças entre as observações antes e depois de uma intervenção). Essas diferenças representam a mudança observada em cada par de observações.
Estatística t (t-statistic): A estatística t é calculada a partir das diferenças, do desvio padrão das diferenças e do número de pares de observações. Ela quantifica a magnitude da diferença média entre as duas amostras em termos de desvios padrão. Quanto maior for a estatística t, maior será a diferença relativa entre as médias.
Graus de Liberdade (degrees of freedom): Os graus de liberdade são usados para calcular o valor-p e indicam quantos graus de liberdade estão disponíveis para o teste estatístico. No teste t pareado, os graus de liberdade são determinados pelo número de pares de observações menos 1.
Valor-p (p-value): O valor-p é a probabilidade de obter um resultado tão extremo ou mais extremo do que o observado, sob a hipótese nula de que não há diferença real entre as duas amostras relacionadas. Quanto menor o valor-p, mais forte é a evidência contra a hipótese nula.
Se o valor-p for menor que o nível de significância escolhido (geralmente definido em 0,05 ou 0,01), você rejeita a hipótese nula (H0) e conclui que existe uma diferença estatisticamente significativa entre as médias das duas amostras relacionadas. Ou seja as médias são diferentes.
Se o valor-p for maior que o nível de significância, você não rejeita a hipótese nula e não tem evidências estatísticas para concluir que as médias são diferentes.
# Criar um dataframe com notas antes e depois do treinamento
antes <- c(75, 82, 68, 90, 77)
depois <- c(85, 88, 72, 94, 80)
dados_t_pareado <- data.frame(antes, depois)
Normalidade:
diferenca <- dados_t_pareado$antes - dados_t_pareado$depois
shapiro.test(diferenca) #Apresenta normalidade p-valor > 0,05
Shapiro-Wilk normality test
data: diferenca
W = 0.8452, p-value = 0.1798
Teste:
# Realizar o teste t pareado
t.test(dados_t_pareado$antes, dados_t_pareado$depois, paired = TRUE) # Apresenta diferença entre os tempos p-valor > 0,05
Paired t-test
data: dados_t_pareado$antes and dados_t_pareado$depois
t = -4.3235, df = 4, p-value = 0.01241
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-8.867779 -1.932221
sample estimates:
mean of the differences
-5.4
Visualização:
# Adicionar uma coluna que represente a ordem das observações
dados_t_pareado$Observacao <- 1:nrow(dados_t_pareado)
# Criar um novo dataframe no formato long (tidy)
if(!require(tidyr)) install.packages("tidyr")
library(tidyr)
dados_tidy <- gather(dados_t_pareado, key = "Tempo", value = "Nota", -Observacao) #Observe que foi realizada uma reorganização dos dados
ggplot(dados_tidy,aes(x=Tempo,y=Nota,group = Observacao)) +
geom_point() +
geom_line() +
coord_cartesian(xlim = c(1.4,1.6)) + # Para deixar os pontos antes e depois mais distantes
theme_classic()
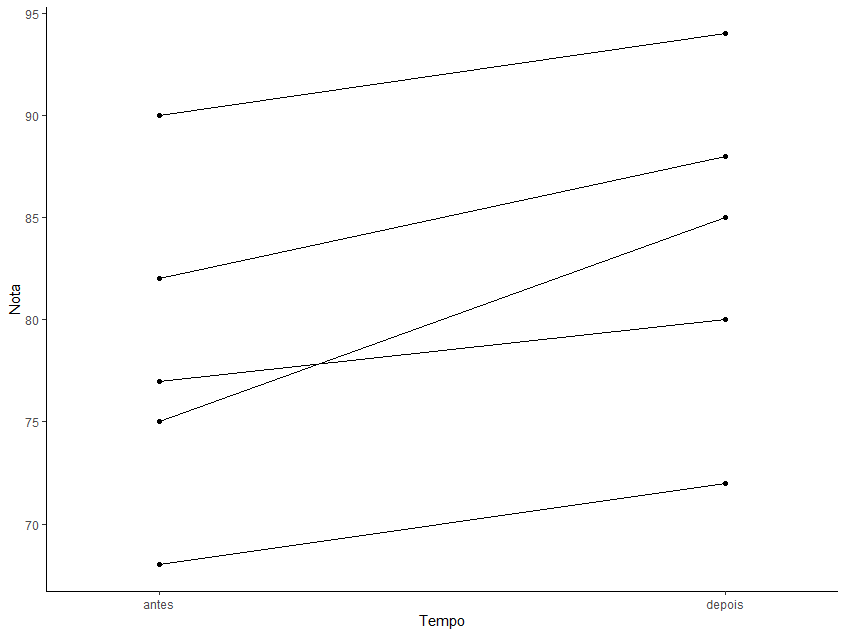
ANOVA
A análise de variância (ANOVA) é uma técnica estatística usada para avaliar se existem diferenças significativas entre as médias de dois ou mais grupos ou populações. A ANOVA compara as variações entre os grupos com as variações dentro dos grupos, permitindo determinar se as diferenças observadas nas médias são provavelmente devidas a fatores reais ou se podem ser atribuídas à aleatoriedade. Existem vários tipos de ANOVA, cada um adequado para diferentes cenários e objetivos de pesquisa. Aqui estão os principais tipos de ANOVA:
- ANOVA de Um Fator (One-Way ANOVA): Também conhecida como ANOVA de um fator, é usada quando você está comparando as médias de três ou mais grupos independentes. Por exemplo, você pode usar a ANOVA de um fator para comparar as médias de desempenho de estudantes de três escolas diferentes.
- ANOVA de Dois Fatores (Two-Way ANOVA): A ANOVA de dois fatores é usada quando você tem duas variáveis independentes (fatores) e deseja avaliar como esses fatores afetam uma variável dependente. Por exemplo, você pode usar a ANOVA de dois fatores para analisar como a dose de um medicamento e o sexo dos pacientes afetam a resposta a um tratamento.
Outros tipos são: ANOVA de Medidas Repetidas (Repeated Measures ANOVA), ANOVA de Variáveis de Bloco (ANCOVA – Analysis of Covariance) e ANOVA Multivariada (MANOVA – Multivariate Analysis of Variance). A interpretação dos resultados da ANOVA envolve a análise do valor-p associado ao teste estatístico. Um valor-p menor que o nível de significância (geralmente definido em 0,05) indica que existe uma diferença estatisticamente significativa entre os grupos (ou condições), permitindo rejeitar a hipótese nula. A escolha do tipo de ANOVA depende da natureza dos seus dados e das suas perguntas de pesquisa. Cada tipo de ANOVA aborda situações específicas e é importante selecionar o método correto para obter resultados confiáveis e interpretáveis.
Abaixo exemplificaremos os testes mais usados de ANOVA (ANOVA de uma via e ANOVA de duas vias).
ANOVA 1 via independente
Uma variável dependente numérica e uma variável categórica com 2 ou mais níveis/grupos.
Normalidade:
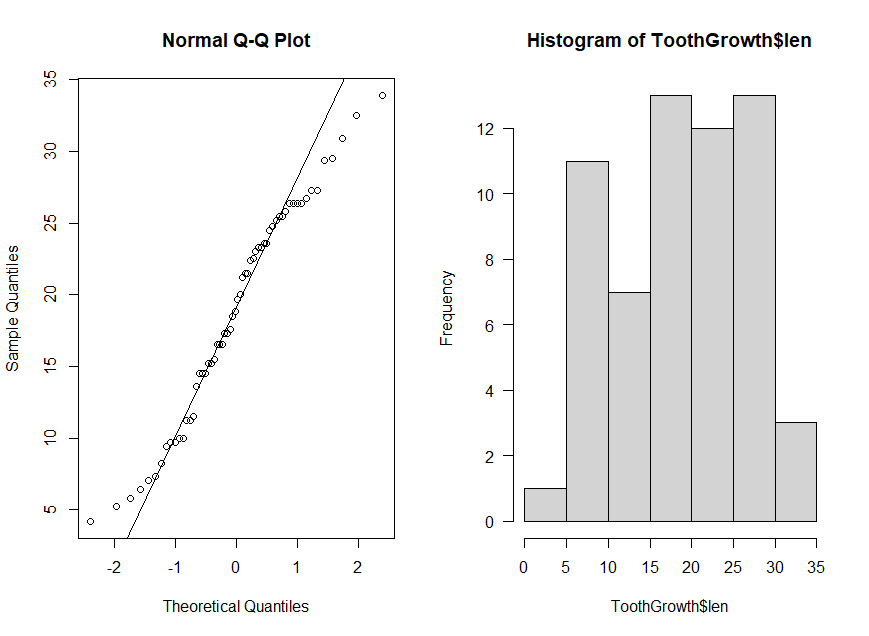
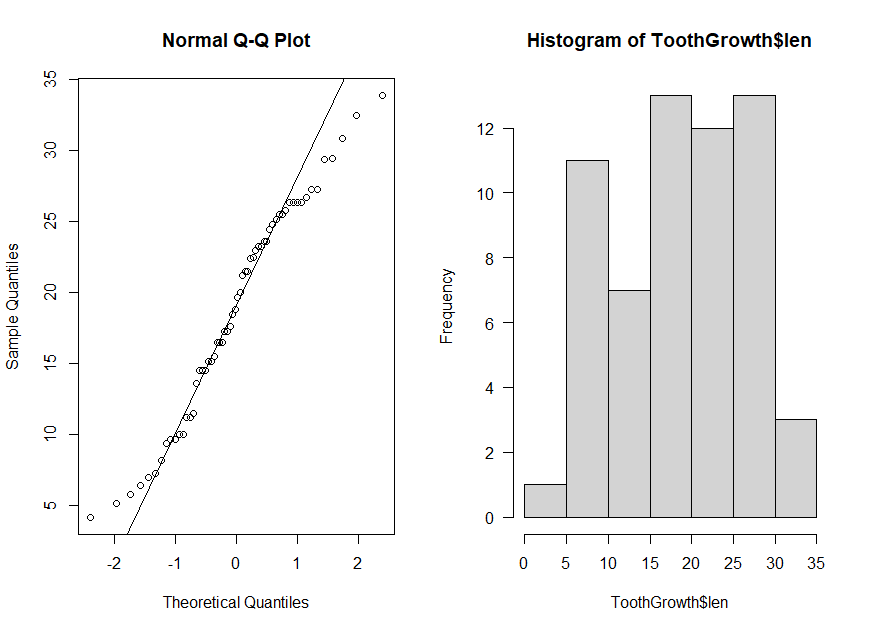
shapiro.test(ToothGrowth$len) # Normal, p-valor > 0,05
par(mfrow=c(1,2))
qqnorm(ToothGrowth$len)
qqline(ToothGrowth$len)
hist(ToothGrowth$len, las=1)
par(mfrow=c(1,1))
Shapiro-Wilk normality test
data: ToothGrowth$len
W = 0.96743, p-value = 0.1091
Homogeneidade das variâncias:
leveneTest(len ~ dose, data = ToothGrowth, center=mean) # Variâncias homogêneas p-valor > 0,05
Levene's Test for Homogeneity of Variance (center = mean)
Df F value Pr(>F)
group 2 0.7328 0.485
57
Teste e visualização dos resíduos
modeloAOV <- aov(len ~ dose, data = ToothGrowth) #Comparando len em relação a dose
summary(modeloAOV) #O Valor de P em Pr(>F), indica que existe diferênça significativa
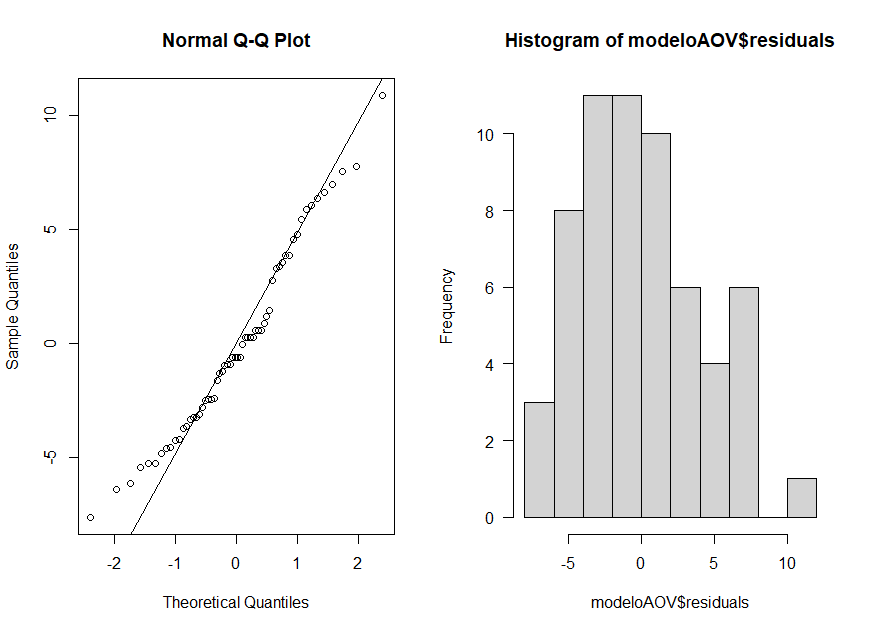
par(mfrow=c(1,2))
qqnorm(modeloAOV$residuals) # Resíduos (rodar modelo antes)
qqline(modeloAOV$residuals) # Resíduos (rodar modelo antes) Visualizando a normalidade dos resíduos da Anova
hist(modeloAOV$residuals, las=1) # Resíduos (rodar modelo antes)
par(mfrow=c(1,1))
Df Sum Sq Mean Sq F value Pr(>F)
dose 2 2426 1213 67.42 9.53e-16 ***
Residuals 57 1026 18
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Análise post-hoc (pacote DescTools)
As funções PostHocTest() com diferentes métodos são usadas para realizar testes de comparações múltiplas após a realização de uma Análise de Variância (ANOVA) para identificar quais grupos específicos diferem entre si. Cada método tem suas próprias características e níveis de correção para controlar o erro tipo I (falso positivo) nas comparações múltiplas. Abaixo estão destacadas as características de cada método.
PostHocTest(modeloAOV, method = “duncan”):
O método “Duncan” é usado para realizar testes de comparações múltiplas após uma ANOVA.
Ele realiza todas as comparações possíveis entre os grupos, calculando diferenças significativas entre as médias.
Este método não aplica correção para múltiplas comparações, o que significa que pode ser mais liberal em identificar diferenças, mas também aumenta o risco de falso positivo. Portanto, é importante usá-lo com cautela e interpretar os resultados com cuidado.
PostHocTest(modeloAOV, method = “hsd”):
O método “HSD” (LSD, sigla em inglês para Least Significant Difference) é outro método para comparações múltiplas após uma ANOVA.
Ele realiza comparações entre todas as combinações de grupos e aplica correção de Tukey para controlar o erro tipo I nas comparações múltiplas.
O teste HSD é mais conservador do que o método de Duncan, o que significa que ele pode ser menos propenso a identificar diferenças significativas, mas é mais rigoroso na correção de múltiplas comparações.
PostHocTest(modeloAOV, method = “bonf”):
O método “Bonferroni” é outro método de correção para comparações múltiplas após uma ANOVA.
Ele ajusta o nível de significância (valor-p) para cada comparação com base no número total de comparações que estão sendo realizadas.
O método Bonferroni é bastante conservador e tende a ser mais restritivo na identificação de diferenças significativas, o que ajuda a controlar o erro tipo I.
A escolha entre esses métodos depende do seu objetivo de pesquisa, do número de comparações que você está realizando e da importância de controlar o erro tipo I. O método Bonferroni é geralmente recomendado quando se deseja um controle rigoroso do erro tipo I, enquanto o método de Duncan pode ser usado quando se deseja explorar diferenças sem fazer correções para múltiplas comparações. O método HSD é um compromisso entre os dois, oferecendo uma correção eficaz para múltiplas comparações sem ser tão conservador quanto o Bonferroni.
if(!require(DescTools)) install.packages("DescTools")
library(DescTools)
PostHocTest(modeloAOV, method = "duncan")
PostHocTest(modeloAOV, method = "hsd")
PostHocTest(modeloAOV, method = "bonf")
#Outra maneira:
TukeyHSD(modeloAOV)
Posthoc multiple comparisons of means : Duncan's new multiple range test
95% family-wise confidence level
$dose
diff lwr.ci upr.ci pval
1-0.5 9.130 6.443705 11.816295 6.7e-09 ***
2-0.5 15.495 12.669231 18.320769 5.6e-12 ***
2-1 6.365 3.678705 9.051295 1.4e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Posthoc multiple comparisons of means : Tukey HSD
95% family-wise confidence level
$dose
diff lwr.ci upr.ci pval
1-0.5 9.130 5.901805 12.358195 2.0e-08 ***
2-0.5 15.495 12.266805 18.723195 1.1e-11 ***
2-1 6.365 3.136805 9.593195 4.2e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Posthoc multiple comparisons of means : Bonferroni
95% family-wise confidence level
$dose
diff lwr.ci upr.ci pval
1-0.5 9.130 5.820955 12.439045 2.0e-08 ***
2-0.5 15.495 12.185955 18.804045 4.4e-16 ***
2-1 6.365 3.055955 9.674045 4.3e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = len ~ dose, data = ToothGrowth)
$dose
diff lwr upr p adj
1-0.5 9.130 5.901805 12.358195 0.00e+00
2-0.5 15.495 12.266805 18.723195 0.00e+00
2-1 6.365 3.136805 9.593195 4.25e-05
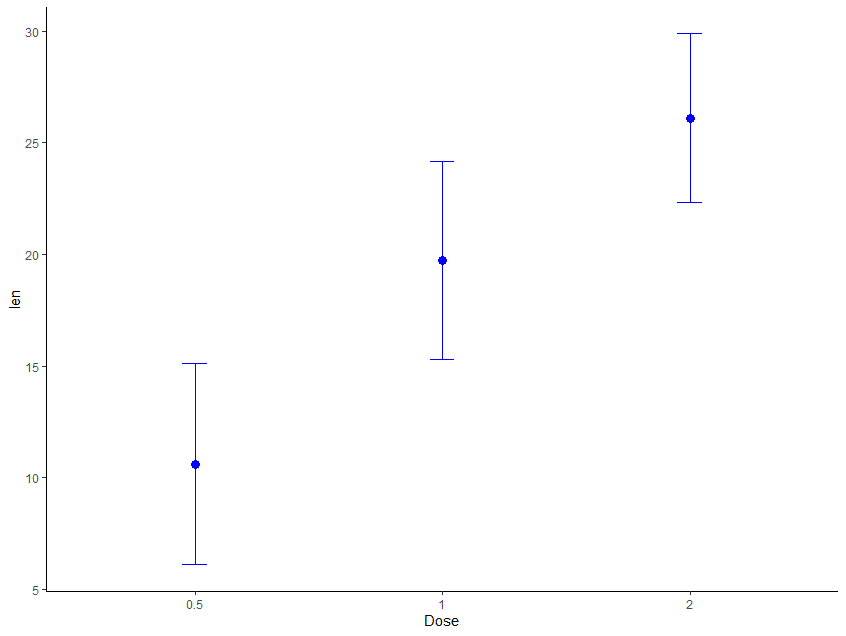
Visualização:
# Criar o gráfico de ponto com média e erro padrão
ggplot(ToothGrowth, aes(x = factor(dose), y = len)) +
stat_summary(fun.data = mean_sdl, fun.args = list(mult = 1),
geom = "point", size = 3, color = "blue") +
stat_summary(fun.data = mean_sdl, fun.args = list(mult = 1),
geom = "errorbar", width = 0.1, color = "blue") +
labs(x = "Dose", y = "len") + theme_classic()
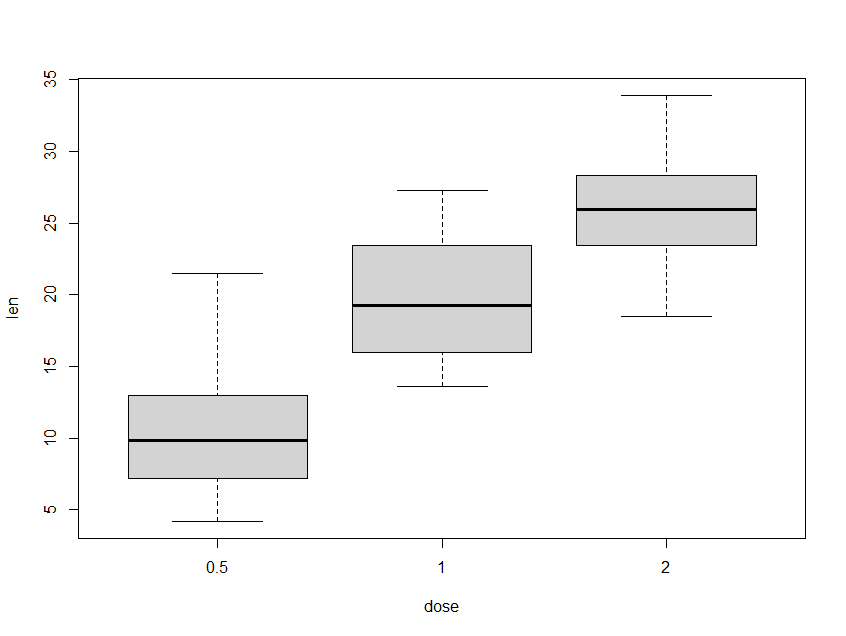
# Boxplot:
boxplot(len ~ dose, data = ToothGrowth, ylab="len", xlab="dose")
ANOVA 2 vias independente
Uma variavel dependente numérica e duas varáveis independentes categóricas.
Pacotes:
if(!require(dplyr)) install.packages("dplyr")
library(dplyr)
if(!require(rstatix)) install.packages("rstatix")
library(rstatix)
if(!require(emmeans)) install.packages("emmeans")
library(emmeans)
Normalidade:
shapiro.test(ToothGrowth$len) #Normal
par(mfrow=c(1,2))
qqnorm(ToothGrowth$len)
qqline(ToothGrowth$len)
hist(ToothGrowth$len, las=1)
par(mfrow=c(1,1))
Shapiro-Wilk normality test
data: ToothGrowth$len
W = 0.96743, p-value = 0.1091
Homogeneidade das variâncias
leveneTest(len ~ supp*dose, ToothGrowth, center = mean) #Variâncias homogêneas p-valor > 0,05
Levene's Test for Homogeneity of Variance (center = mean)
Df F value Pr(>F)
group 5 1.9401 0.1027
54
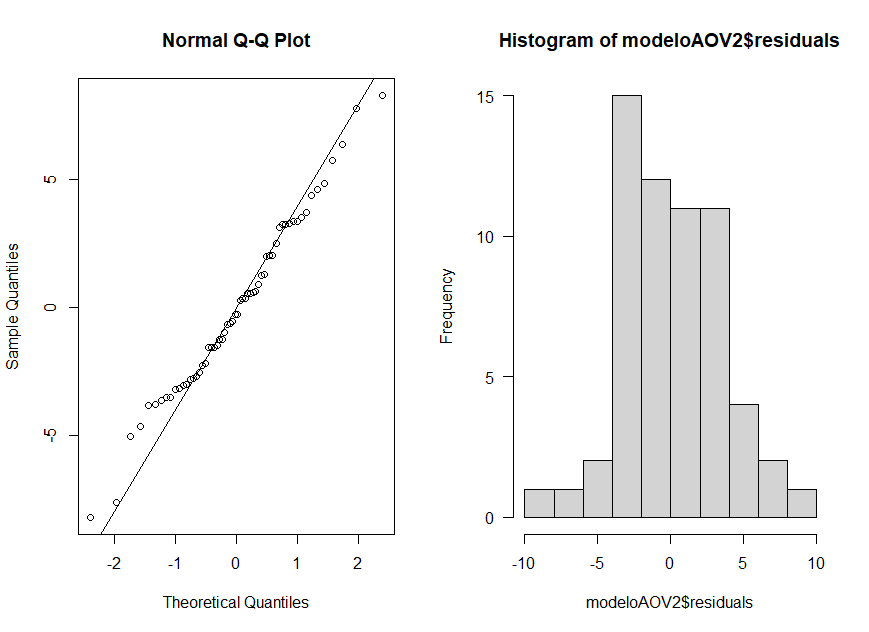
Modelo e visualização da normalidade dos resíduos:
modeloAOV2 <- aov(len ~ supp*dose, ToothGrowth)
par(mfrow=c(1,2))
qqnorm(modeloAOV2$residuals) # Resíduos (rodar modelo antes)
qqline(modeloAOV2$residuals) # Resíduos (rodar modelo antes)
hist(modeloAOV2$residuals, las=1) # Resíduos (rodar modelo antes)
par(mfrow=c(1,1))
modeloAOV2s <- aov(len ~ supp+dose, ToothGrowth) # Com o + em vez de * é possível delimitar quais as comparações que devem ser análisadas, observe abaixo nos resultados
Resultado ANOVA
summary(modeloAOV2)
summary(modeloAOV2s)
Df Sum Sq Mean Sq F value Pr(>F)
supp 1 205.4 205.4 15.572 0.000231 ***
dose 2 2426.4 1213.2 92.000 < 2e-16 ***
supp:dose 2 108.3 54.2 4.107 0.021860 *
Residuals 54 712.1 13.2
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Df Sum Sq Mean Sq F value Pr(>F)
supp 1 205.4 205.4 14.02 0.000429 ***
dose 2 2426.4 1213.2 82.81 < 2e-16 ***
Residuals 56 820.4 14.7
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
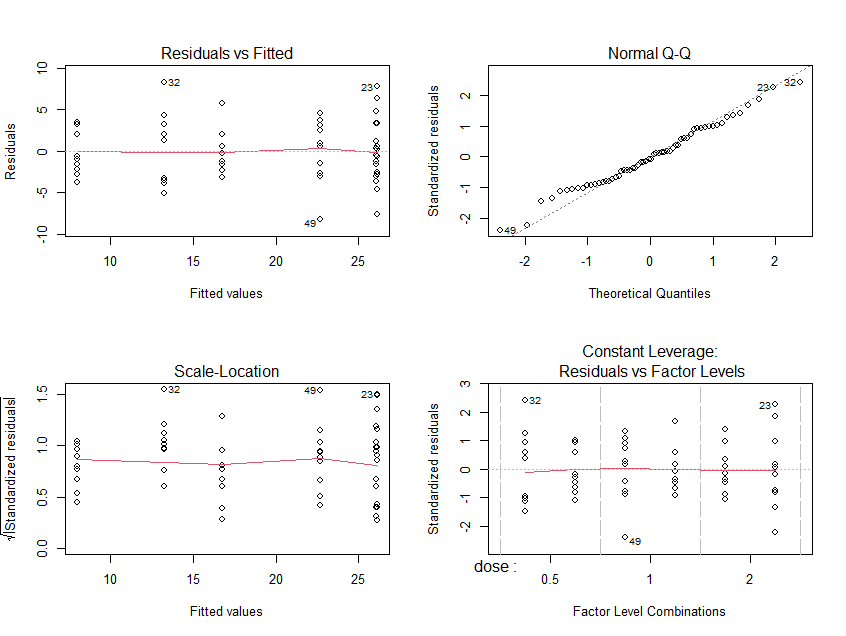
Para avaliar se o modelo está adequado podem ser utilizados gráficos de diagnóstico Saiba mais.
par(mfrow=c(2,2))
plot(aov(ToothGrowth[,'len']~dose*supp,
ToothGrowth,na.action=na.omit))
par(mfrow=c(1,1))
PostHoc
Supp:
ToothGrowth %>% group_by(supp) %>%
emmeans_test(len ~ dose, p.adjust.method = "bonferroni")
# A tibble: 6 x 10
supp term .y. group1 group2 df statistic p p.adj p.adj.signif
* <fct> <chr> <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <chr>
1 OJ dose len 0.5 1 54 -5.83 3.18e- 7 9.53e- 7 ****
2 OJ dose len 0.5 2 54 -7.90 1.43e-10 4.29e-10 ****
3 OJ dose len 1 2 54 -2.07 4.34e- 2 1.30e- 1 ns
4 VC dose len 0.5 1 54 -5.41 1.46e- 6 4.39e- 6 ****
5 VC dose len 0.5 2 54 -11.2 1.13e-15 3.39e-15 ****
6 VC dose len 1 2 54 -5.77 3.98e- 7 1.19e- 6 ****
Dose:
ToothGrowth %>% group_by(dose) %>%
emmeans_test(len ~ supp, p.adjust.method = "bonferroni")
# A tibble: 3 x 10
dose term .y. group1 group2 df statistic p p.adj p.adj.signif
* <fct> <chr> <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <chr>
1 0.5 supp len OJ VC 54 3.23 0.00209 0.00209 **
2 1 supp len OJ VC 54 3.65 0.000590 0.000590 ***
3 2 supp len OJ VC 54 -0.0493 0.961 0.961 ns
Pacote DescTools: Opções: “hsd”, “bonferroni”, “lsd”, “scheffe”, “newmankeuls”, “duncan”
PostHocTest(modeloAOV2, method = "duncan")
Posthoc multiple comparisons of means : Duncan's new multiple range test
95% family-wise confidence level
$supp
diff lwr.ci upr.ci pval
VC-OJ -3.7 -5.579828 -1.820172 0.00023 ***
$dose
diff lwr.ci upr.ci pval
1-0.5 9.130 6.827691 11.432309 1.2e-10 ***
2-0.5 15.495 13.073289 17.916711 2.2e-13 ***
2-1 6.365 4.062691 8.667309 9.1e-07 ***
$`supp:dose`
diff lwr.ci upr.ci pval
VC:0.5-OJ:0.5 -5.25 -8.50595707 -1.994043 0.00209 **
OJ:1-OJ:0.5 9.47 6.04518392 12.894816 4.7e-07 ***
VC:1-OJ:0.5 3.54 0.28404293 6.795957 0.03365 *
OJ:2-OJ:0.5 12.83 9.29399005 16.366010 2.8e-10 ***
VC:2-OJ:0.5 12.91 9.29325843 16.526742 3.0e-10 ***
OJ:1-VC:0.5 14.72 11.18399005 18.256010 4.1e-12 ***
VC:1-VC:0.5 8.79 5.36518392 12.214816 2.2e-06 ***
OJ:2-VC:0.5 18.08 14.46325843 21.696742 1.2e-13 ***
VC:2-VC:0.5 18.16 14.48118308 21.838817 9.6e-14 ***
VC:1-OJ:1 -5.93 -9.18595707 -2.674043 0.00059 ***
OJ:2-OJ:1 3.36 0.10404293 6.615957 0.04335 *
VC:2-OJ:1 3.44 0.01518392 6.864816 0.04900 *
OJ:2-VC:1 9.29 5.86518392 12.714816 7.1e-07 ***
VC:2-VC:1 9.37 5.83399005 12.906010 7.8e-07 ***
VC:2-OJ:2 0.08 -3.17595707 3.335957 0.96089
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
PostHocTest(modeloAOV2, method = "hsd")
Posthoc multiple comparisons of means : Tukey HSD
95% family-wise confidence level
$supp
diff lwr.ci upr.ci pval
VC-OJ -3.7 -5.579828 -1.820172 0.00023 ***
$dose
diff lwr.ci upr.ci pval
1-0.5 9.130 6.362488 11.897512 3.6e-10 ***
2-0.5 15.495 12.727488 18.262512 4.4e-13 ***
2-1 6.365 3.597488 9.132512 2.7e-06 ***
$`supp:dose`
diff lwr.ci upr.ci pval
VC:0.5-OJ:0.5 -5.25 -10.048124 -0.4518762 0.0243 *
OJ:1-OJ:0.5 9.47 4.671876 14.2681238 4.6e-06 ***
VC:1-OJ:0.5 3.54 -1.258124 8.3381238 0.2640
OJ:2-OJ:0.5 12.83 8.031876 17.6281238 2.1e-09 ***
VC:2-OJ:0.5 12.91 8.111876 17.7081238 1.8e-09 ***
OJ:1-VC:0.5 14.72 9.921876 19.5181238 3.0e-11 ***
VC:1-VC:0.5 8.79 3.991876 13.5881238 2.1e-05 ***
OJ:2-VC:0.5 18.08 13.281876 22.8781238 4.9e-13 ***
VC:2-VC:0.5 18.16 13.361876 22.9581238 4.8e-13 ***
VC:1-OJ:1 -5.93 -10.728124 -1.1318762 0.0074 **
OJ:2-OJ:1 3.36 -1.438124 8.1581238 0.3187
VC:2-OJ:1 3.44 -1.358124 8.2381238 0.2936
OJ:2-VC:1 9.29 4.491876 14.0881238 6.9e-06 ***
VC:2-VC:1 9.37 4.571876 14.1681238 5.8e-06 ***
VC:2-OJ:2 0.08 -4.718124 4.8781238 1.0000
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
PostHocTest(modeloAOV2, method = "bonferroni")
Posthoc multiple comparisons of means : Bonferroni
95% family-wise confidence level
$supp
diff lwr.ci upr.ci pval
VC-OJ -3.7 -5.579828 -1.820172 0.00023 ***
$dose
diff lwr.ci upr.ci pval
1-0.5 9.130 6.292594 11.967406 3.6e-10 ***
2-0.5 15.495 12.657594 18.332406 < 2e-16 ***
2-1 6.365 3.527594 9.202406 2.7e-06 ***
$`supp:dose`
diff lwr.ci upr.ci pval
VC:0.5-OJ:0.5 -5.25 -10.238008 -0.2619924 0.0314 *
OJ:1-OJ:0.5 9.47 4.481992 14.4580076 4.8e-06 ***
VC:1-OJ:0.5 3.54 -1.448008 8.5280076 0.5048
OJ:2-OJ:0.5 12.83 7.841992 17.8180076 2.1e-09 ***
VC:2-OJ:0.5 12.91 7.921992 17.8980076 1.8e-09 ***
OJ:1-VC:0.5 14.72 9.731992 19.7080076 3.0e-11 ***
VC:1-VC:0.5 8.79 3.801992 13.7780076 2.2e-05 ***
OJ:2-VC:0.5 18.08 13.091992 23.0680076 2.0e-14 ***
VC:2-VC:0.5 18.16 13.171992 23.1480076 1.7e-14 ***
VC:1-OJ:1 -5.93 -10.918008 -0.9419924 0.0088 **
OJ:2-OJ:1 3.36 -1.628008 8.3480076 0.6503
VC:2-OJ:1 3.44 -1.548008 8.4280076 0.5816
OJ:2-VC:1 9.29 4.301992 14.2780076 7.2e-06 ***
VC:2-VC:1 9.37 4.381992 14.3580076 6.0e-06 ***
VC:2-OJ:2 0.08 -4.908008 5.0680076 1.0000
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
TukeyHSD(modeloAOV2) # Outra opção
Posthoc multiple comparisons of means : Tukey HSD
95% family-wise confidence level
$supp
diff lwr.ci upr.ci pval
VC-OJ -3.7 -5.579828 -1.820172 0.00023 ***
$dose
diff lwr.ci upr.ci pval
1-0.5 9.130 6.362488 11.897512 3.6e-10 ***
2-0.5 15.495 12.727488 18.262512 4.4e-13 ***
2-1 6.365 3.597488 9.132512 2.7e-06 ***
$`supp:dose`
diff lwr.ci upr.ci pval
VC:0.5-OJ:0.5 -5.25 -10.048124 -0.4518762 0.0243 *
OJ:1-OJ:0.5 9.47 4.671876 14.2681238 4.6e-06 ***
VC:1-OJ:0.5 3.54 -1.258124 8.3381238 0.2640
OJ:2-OJ:0.5 12.83 8.031876 17.6281238 2.1e-09 ***
VC:2-OJ:0.5 12.91 8.111876 17.7081238 1.8e-09 ***
OJ:1-VC:0.5 14.72 9.921876 19.5181238 3.0e-11 ***
VC:1-VC:0.5 8.79 3.991876 13.5881238 2.1e-05 ***
OJ:2-VC:0.5 18.08 13.281876 22.8781238 4.9e-13 ***
VC:2-VC:0.5 18.16 13.361876 22.9581238 4.8e-13 ***
VC:1-OJ:1 -5.93 -10.728124 -1.1318762 0.0074 **
OJ:2-OJ:1 3.36 -1.438124 8.1581238 0.3187
VC:2-OJ:1 3.44 -1.358124 8.2381238 0.2936
OJ:2-VC:1 9.29 4.491876 14.0881238 6.9e-06 ***
VC:2-VC:1 9.37 4.571876 14.1681238 5.8e-06 ***
VC:2-OJ:2 0.08 -4.718124 4.8781238 1.0000
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
> PostHocTest(modeloAOV2, method = "bonferroni")
Posthoc multiple comparisons of means : Bonferroni
95% family-wise confidence level
$supp
diff lwr.ci upr.ci pval
VC-OJ -3.7 -5.579828 -1.820172 0.00023 ***
$dose
diff lwr.ci upr.ci pval
1-0.5 9.130 6.292594 11.967406 3.6e-10 ***
2-0.5 15.495 12.657594 18.332406 < 2e-16 ***
2-1 6.365 3.527594 9.202406 2.7e-06 ***
$`supp:dose`
diff lwr.ci upr.ci pval
VC:0.5-OJ:0.5 -5.25 -10.238008 -0.2619924 0.0314 *
OJ:1-OJ:0.5 9.47 4.481992 14.4580076 4.8e-06 ***
VC:1-OJ:0.5 3.54 -1.448008 8.5280076 0.5048
OJ:2-OJ:0.5 12.83 7.841992 17.8180076 2.1e-09 ***
VC:2-OJ:0.5 12.91 7.921992 17.8980076 1.8e-09 ***
OJ:1-VC:0.5 14.72 9.731992 19.7080076 3.0e-11 ***
VC:1-VC:0.5 8.79 3.801992 13.7780076 2.2e-05 ***
OJ:2-VC:0.5 18.08 13.091992 23.0680076 2.0e-14 ***
VC:2-VC:0.5 18.16 13.171992 23.1480076 1.7e-14 ***
VC:1-OJ:1 -5.93 -10.918008 -0.9419924 0.0088 **
OJ:2-OJ:1 3.36 -1.628008 8.3480076 0.6503
VC:2-OJ:1 3.44 -1.548008 8.4280076 0.5816
OJ:2-VC:1 9.29 4.301992 14.2780076 7.2e-06 ***
VC:2-VC:1 9.37 4.381992 14.3580076 6.0e-06 ***
VC:2-OJ:2 0.08 -4.908008 5.0680076 1.0000
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
> TukeyHSD(modeloAOV2)
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = len ~ supp * dose, data = ToothGrowth)
$supp
diff lwr upr p adj
VC-OJ -3.7 -5.579828 -1.820172 0.0002312
$dose
diff lwr upr p adj
1-0.5 9.130 6.362488 11.897512 0.0e+00
2-0.5 15.495 12.727488 18.262512 0.0e+00
2-1 6.365 3.597488 9.132512 2.7e-06
$`supp:dose`
diff lwr upr p adj
VC:0.5-OJ:0.5 -5.25 -10.048124 -0.4518762 0.0242521
OJ:1-OJ:0.5 9.47 4.671876 14.2681238 0.0000046
VC:1-OJ:0.5 3.54 -1.258124 8.3381238 0.2640208
OJ:2-OJ:0.5 12.83 8.031876 17.6281238 0.0000000
VC:2-OJ:0.5 12.91 8.111876 17.7081238 0.0000000
OJ:1-VC:0.5 14.72 9.921876 19.5181238 0.0000000
VC:1-VC:0.5 8.79 3.991876 13.5881238 0.0000210
OJ:2-VC:0.5 18.08 13.281876 22.8781238 0.0000000
VC:2-VC:0.5 18.16 13.361876 22.9581238 0.0000000
VC:1-OJ:1 -5.93 -10.728124 -1.1318762 0.0073930
OJ:2-OJ:1 3.36 -1.438124 8.1581238 0.3187361
VC:2-OJ:1 3.44 -1.358124 8.2381238 0.2936430
OJ:2-VC:1 9.29 4.491876 14.0881238 0.0000069
VC:2-VC:1 9.37 4.571876 14.1681238 0.0000058
VC:2-OJ:2 0.08 -4.718124 4.8781238 1.0000000
Visualização:
ggplot(data=ToothGrowth, aes(x=dose, y=len,
fill=supp, color=supp)) +
stat_summary(fun.data="mean_sdl", fun.args = list(mult=1),geom = "errorbar",
position = position_dodge(0.4), width=.2) +
stat_summary(fun=mean, geom= "point", position = position_dodge(0.4))+
scale_x_discrete(name ="Dose") + theme_classic()
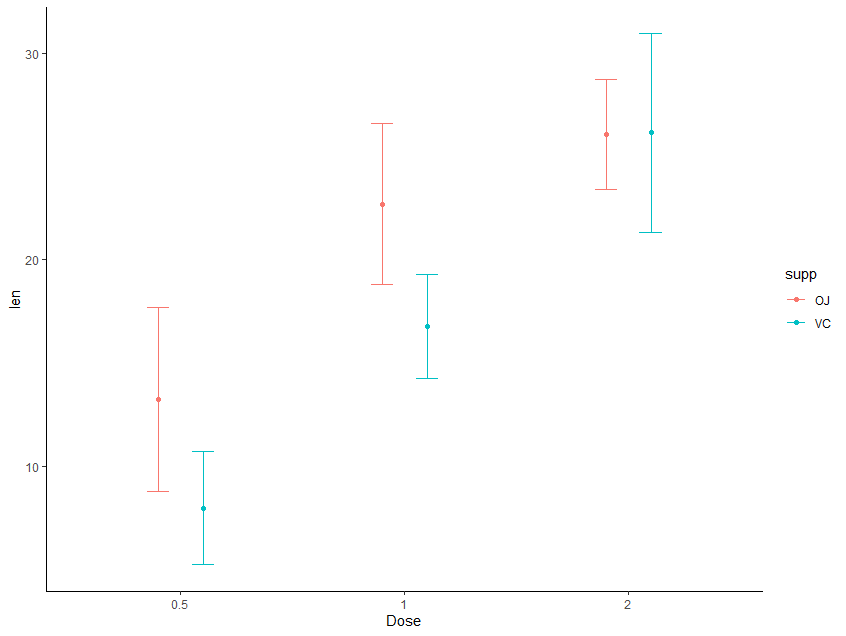
Existem outros testes estatísticos que não foram abordados, mas serão adicionados nos conteúdos extras em breve.
Exercícios
A- Crie um conjunto de dados com uma variável numérica e pelo menos duas variáveis categóricas com mais de um nível cada.
B- Teste a normalidade e homogeneidade da variância dos seus dados.
C- Realize uma anova de 2 vias com seus conjunto de dados.
d- Represente graficamente sua análise.


